Function Practice - Integration with Graphs

The goal of this post is to create a simple function which approximates a definite integral using the trapezoid method and then graphs the original function along with the integration result. We do everything with base R using no packages. While we will not worry about error estimation the user is able to specify the number of partitions used for their integral estimate. Below we have our function graphii:

graphii <- function(FUN, a, b, npart = 100, graph = TRUE) {
  # This is a simple function designed to approximate a definite integral
  # for a continuous function, FUN, over the interval [a, b]. The user
  # should specify the number of partitions, npart, if they want higher
  # accuracy to the approximation. By default npart = 100.
  
  # Our integration algorith is based on the trapezoid method.
  
  pl <- (b - a) / npart # partition length
  pp <- seq(a, b, pl) # partition points
  
  sum = 0
  for (i in 1:npart) {
    sum = sum + (.5 * pl) * (FUN(pp[i]) + FUN(pp[i+1]))
  }
  
  if (graph == TRUE) {
    x <- seq(a, b, pl)
    y <- vapply(x, FUN = FUN, FUN.VALUE = numeric(1))
    save_plot <- plot(x, y, type = "n")
    points(c(x[1],x[npart+1]), c(y[1], y[npart+1]))
    lines(x,y)
    return(list(sum, save_plot))
  }
  else
    return(sum)
}

We now test our function out on two simple functions \(f_1(x) = x^2\) and \(f_2(x) = \sin(x)\).

function1 = function(x) {x^2}
function2 = function(x) {sin(x)}

We first solve the integral \(\displaystyle \int_0^3 x^2 \ dx\) with the default 100 partitions and then again without a graph using 10000 partitions. The true value for the integral is \(9\).

# test our integration function
graphii(function1, 0, 3)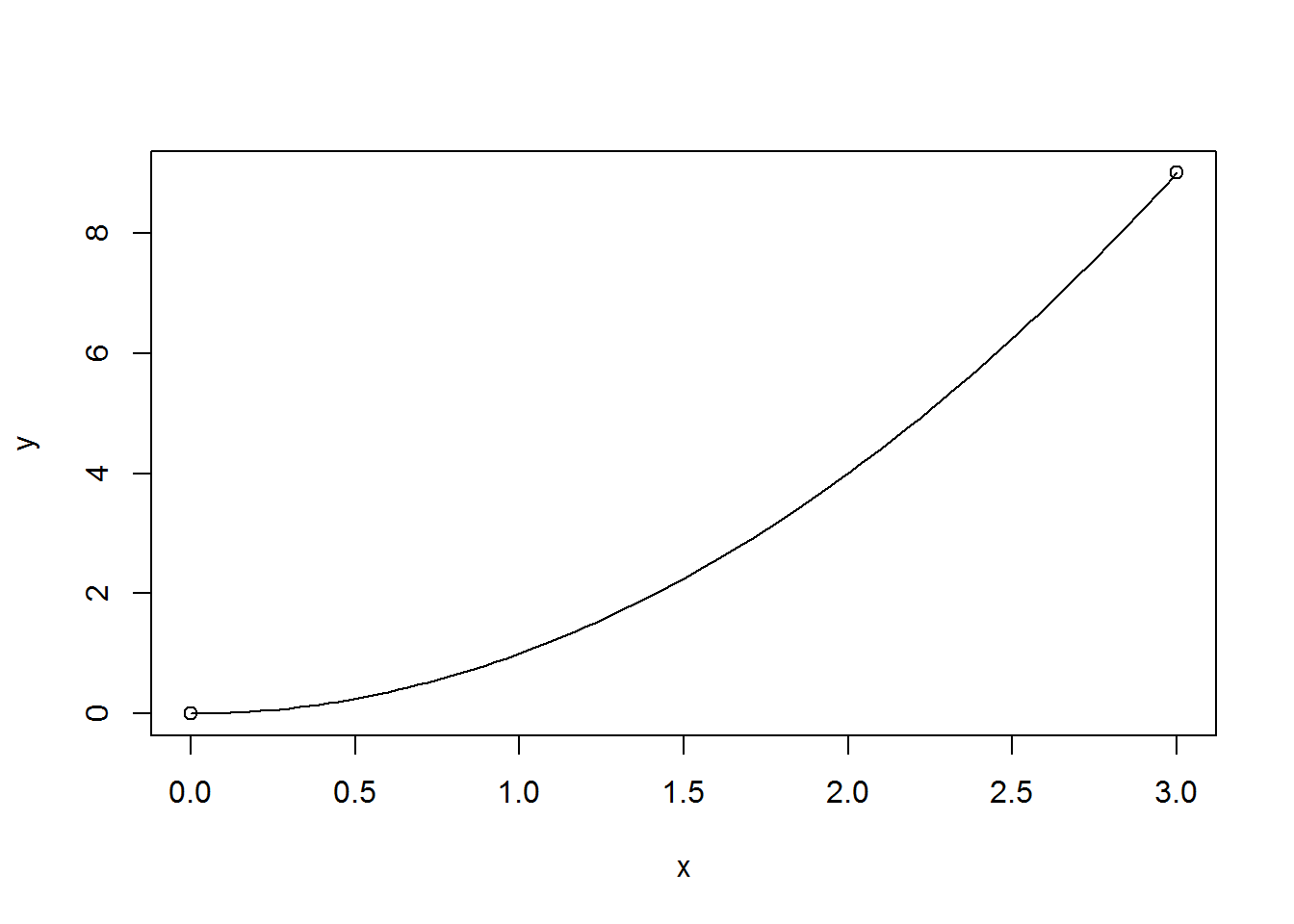

## [[1]]
## [1] 9.00045
## 
## [[2]]
## NULL

graphii(function1, 0, 3, npart = 10000, graph = FALSE)

## [1] 9

We now test our function for approximating the integral \(\displaystyle \int_0^{\pi} \sin{x} \ dx\) using 100 partitions of the given interval.

graphii(function2, 0, pi)

## [[1]]
## [1] 1.999836
## 
## [[2]]
## NULL

Finally we approximate the integral \(\displaystyle \int_1^5 \bigg(\frac{1}{x} + \frac{3}{4}x^3 \bigg)(x-3)^3 \ dx\)

graphii(function(x) {(1/x + (3*x)/4)*(x-3)^3}, 1, 5, npart = 500)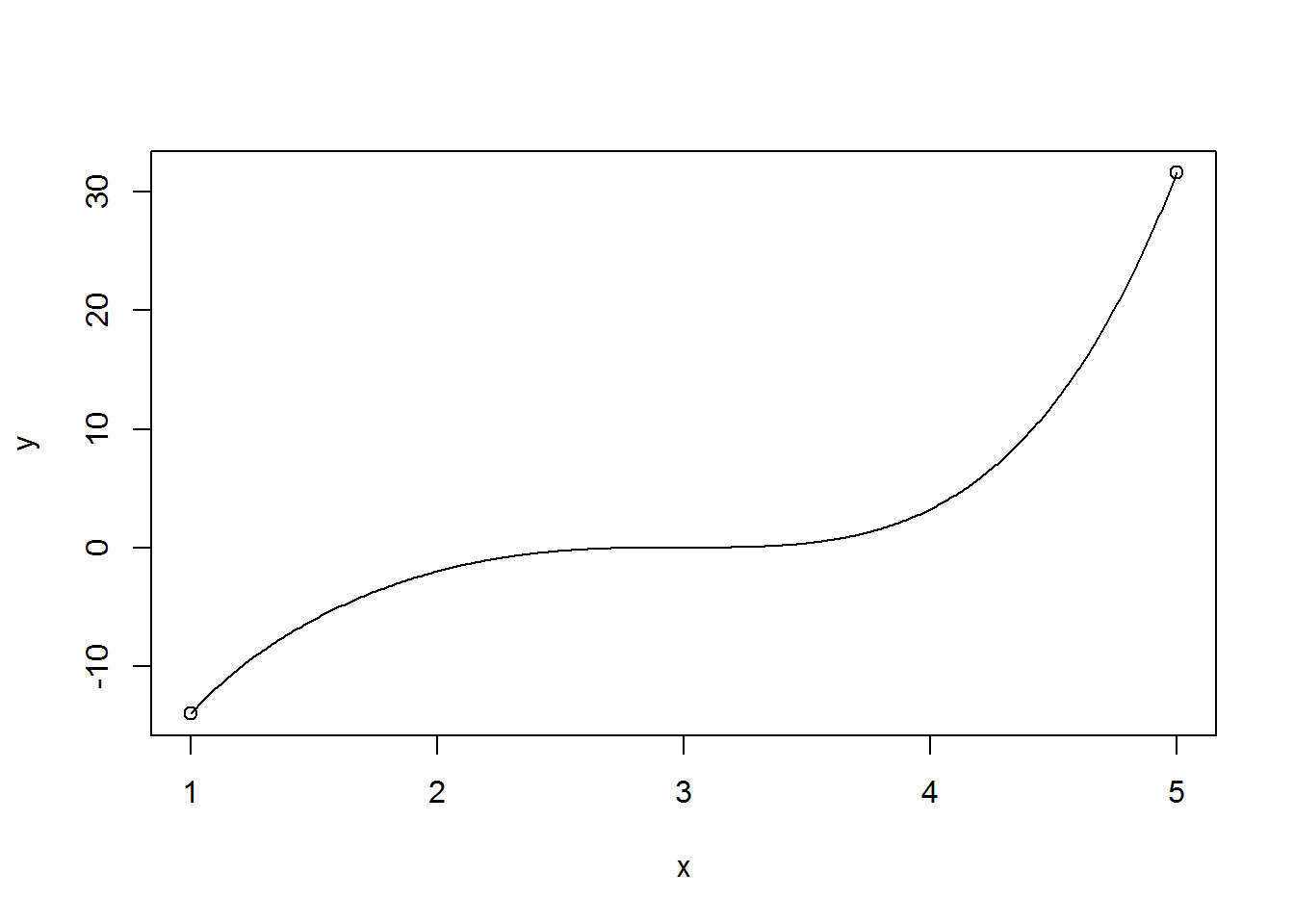

## [[1]]
## [1] 7.47867
## 
## [[2]]
## NULL

This concludes our simple function creation. Future improvements could involve error estimation, more graphical customization, or perhaps using a more sophisticated integration algorithm.